Предмет: Математика
Автор: JuliaKovalchook
Вопрос задан 9 лет назад

Виберіть одну правильну відповідь. Поясніть свій вибір.
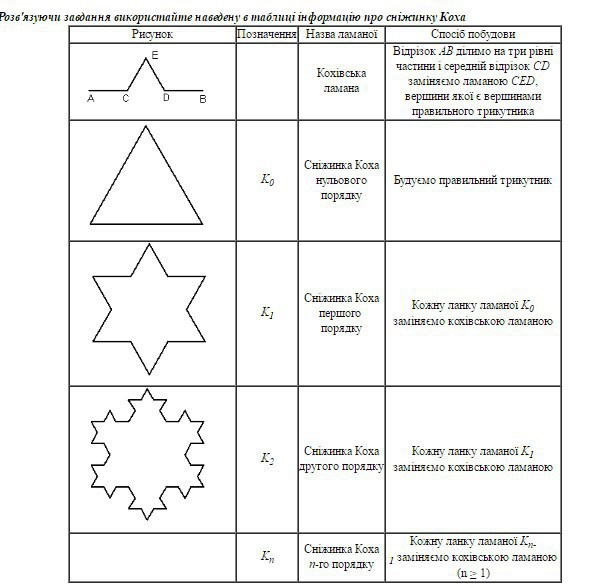
Якщо S — площа трикутника, обмеженого сніжинкою Коха нульового порядку, то площа плоского многокутника, обмеженого сніжинкою Коха першого порядку, дорівнює:
$A) 2S \ \ B) frac{2}{3}S \ \ C) frac{3}{2}S \ \ D) frac{3}{4} S \ \ E) ~~frac{4}{3} S$

Приложения:

Ответы

Ответ дал: NNNLLL54

Многоугольник, ограниченный снежинкой Коха 1 порядка равен площади снежинки Коха 0 порядка плюс три площади равносторонних треугольников, стороны которых равны 1/3 стороны снежинки Коха 0 порядка , то есть а/3.
Площадь равностороннего треугольника равна $S= frac{a^2sqrt3}{4}$ , где a - сторона снежинки Коха 0 порядка.
Площади маленьких равносторонних треугольников со сторонами а/3 равны:

$S^*= frac{(frac{a}{3})^2sqrt3}{4} = frac{a^2sqrt3}{9cdot 4}$

Тогда площадь снежинки Коха 1 порядка равна

$S+3cdot S^*= frac{a^2sqrt3}{4} +3cdot frac{a^2sqrt3}{9cdot 4}= frac{a^2sqrt3}{4} + frac{a^2sqrt3}{3cdot 4} = frac{a^2sqrt3}{4} + frac{a^2sqrt3}{4}cdot frac{1}{3} =\\=S+Scdot frac{1}{3}=frac{4}{3}S$

Ответ дал: JuliaKovalchook

Спасибо

Похожие вопросы

Русский язык

2 года назад

в каком слове звуков больше чем букв просьба июльский Якутия яростный

Русский язык

2 года назад

выписать 10 полных причастий

Алгебра

7 лет назад

Катер по течению за 4 ч. проплыл такое же расстояние, которое проплывает за 6 ч. против течения. Скорость течения реки равна 3 км/ч. Вычисли скорость катера в стоячей воде. Скорость катера в