а) Решить уравнение cos(2x) + 3sin^2(x) = 1,25 б) найдите корни, принадлежащие отрезку [π 5π/2]

Обьясните мне только как решать б). Ответ есть, вы мне только обьясните почему именно так

Используя формулу косинуса двойного угла, сведем данное уравнение к квадратному относительно переменной синус х (так как фигурирует в уравнении квадрат синуса)

отсюда либо k є Z

либо n є Z

обьединяя k  є Z

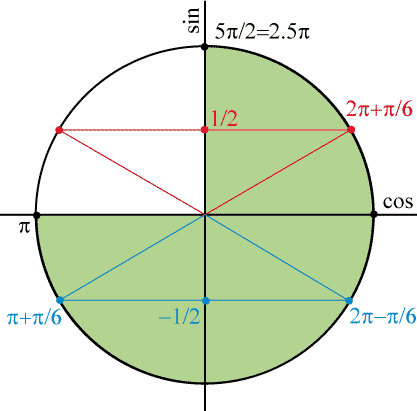
обозначив на кругу, и учититывая нужный указанный промежуток находим корни