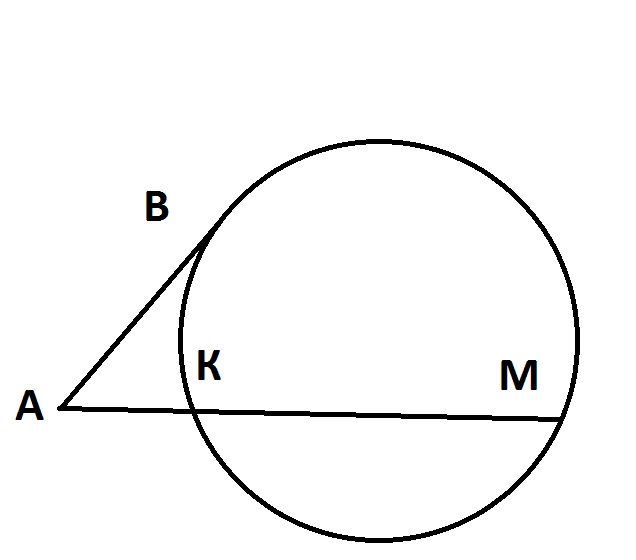
Через точку А к окружности проведена касательная АВ(В-точка касания) и секущая, которая пересекает окружность в точках К и М. Найдите АМ, если КМ:АК=3:1 , АВ=12 см.

В данном случае есть такая формула




Из соотношения в условии задачи. Пусть АК=х см, тогда КМ=3х см. АМ=АК+КМ=х+3х=4х см. Подставим в (*).

Тогда








По смыслу задачи x=6 см. Отрицательного значения быть не может.

АМ=4х=24 см.

Ответ 24 см.

По свойству секущей и касательной проведенные с одной точки 
AB^2=AM*AK