Предмет: Геометрия
Автор: andrewkuza
Вопрос задан 1 год назад

Стороны треугольника равны 11 см, 13 см и 20 см. Через вершину малейшего угла проведен перпендикуляр к плоскости треугольника, а с его конца, не принадлежит треугольнику, опущен перпендикуляр длиной 24 см на противоположную этом углу сторону. Найдите длину перпендикуляра, проведенного к плоскости треугольника.

Ответы

Ответ дал: artalex74

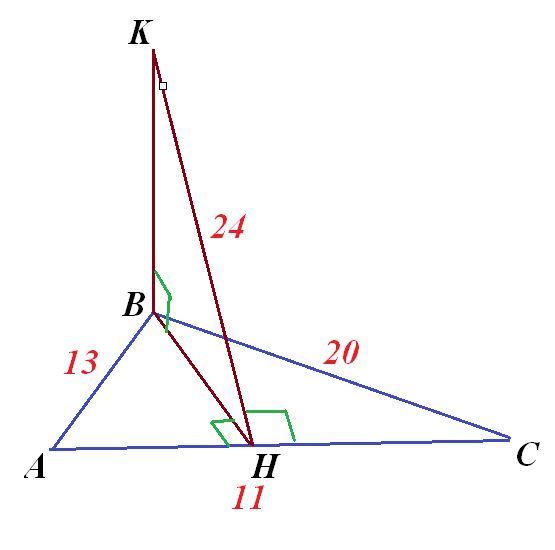
Пусть дан ΔАВС, АВ=13, ВС=20, АС=11.
В треугольнике меньший угол лежит против меньшей стороны.
Значит, данный перпендикуляр к влоскости Δ - это КВ.
Перпендикуляр из точки К на сторону АС - это КН=24. Он является наклонной к перпендикуляру КВ. Тогда ВН - проекция КН на плоскость ΔАВС. По теореме о трёх перпендикулярах ВН⊥АС.
Значит, ВН - высота ΔАВС.
По формуле Герона:
$S_{\Delta}= \sqrt{p(p-a)(p-b)(p-c)} ,\ p= \frac{a+b+c}{2}$
$p= \frac{11+13+20}{2}=22$
$S_{\Delta}= \sqrt{22(22-11)(22-13)(22-20)} = \sqrt{22^2*9}=22*3=66(_{CM^2})$
C др. стороны $S_{\Delta}= \frac{1}{2} AC*BH\ \Rightarrow\ BH= \frac{2S}{AC}= \frac{2*66}{11} =12$
Из прямоугольного ΔКВН по теореме Пифагора КВ²=КН²-ВН²
$KB= \sqrt{24^2-12^2}= \sqrt{12^2(2^2-1)} =12 \sqrt{3}$
Ответ: $12 \sqrt{3}$ см.