С некоторой точки до плоскости проведены две наклонные, длины которых относятся как 5: 6. Найдите длину перпендикуляра, проведенного с этой точки до плоскости, если проекции наклонных равны 3√3 см и 4 см.

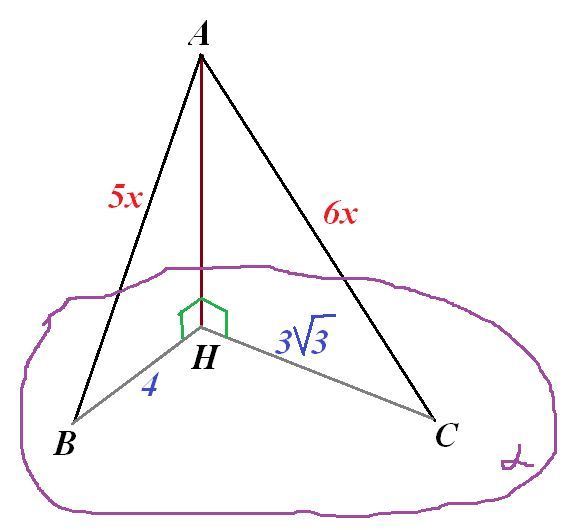
Пусть АВ и АС - наклонные к плоскости α. АН⊥α.
Пусть х - коэффициент пропорциональности. Тогда АВ=5х, АС=6х.
Т.к. AC>AB, то CH>BH.
В прямоугольном ΔАНВ по теореме Пифагора АН² = АВ²-ВН².
В прямоугольном ΔАНС по теореме Пифагора АН² = АС²-СН².
Значит, АВ²-ВН² = АС²-СН².

Ответ: