Помогите! Дам 45 баллов.

1) точка соприкосновения вписанного в ромб круга делит его сторону на отрезки 16 см и 9 см. вычислите диаметр круга.

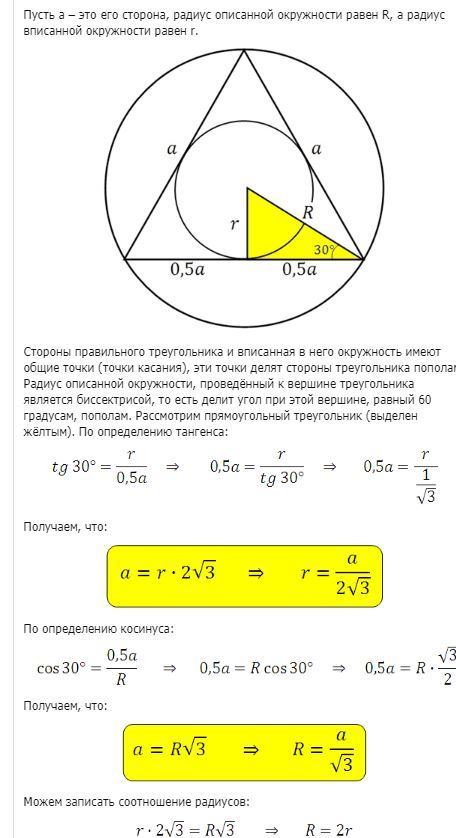
2) найдите отношение площади круга, вписанного в правильный треугольник, к площади круга, описанного вокруг него.

3) сторона ромба равна 25 см, а радиус вписанной в него окружности равен 12 см. вычислите длины отрезков, на которые делит эту сторону точка соприкосновения вписанной окружности