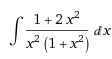Ответы
Ответ дал:
0
Найти интеграл

Решение
Для нахождения интеграла дробь под знаком интеграла представим в виде суммы более простых дробей

Подставим полученную сумму в интеграл


Ответ: arctg(x) - 1/x + C
Решение
Для нахождения интеграла дробь под знаком интеграла представим в виде суммы более простых дробей
Подставим полученную сумму в интеграл
Ответ: arctg(x) - 1/x + C
Похожие вопросы
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад