ПОЖАЙЛУСТА, ОЧЕНЬ НАДО!

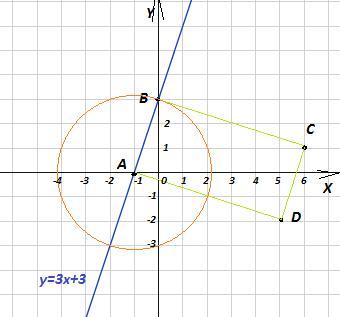
Даны точки А( -1;0), В(0; 3), С(6; 1)
1.а) найдите координат и длину вектора АВ.
   б) разложите вектор АВ по координатным векторам i (вектор) и j (вектор). 
2. а) напишите уравнение окружности с центром в точке А и радиусом АВ.
    б) принадлежит ли этой окружности точка D(5; -2) ?
3. напишите уравнение прямой АВ.
4. а) докажите, что векторы АВ и СД коллинеарны.
    б) Докажите, что АВСД - прямоугольник.

А(-1; 0),  В(0; 3),  С(6; 1)

1.а)

1.б)  

2.a) Общий вид окружности с центром в точке  (x₀; y₀) и радиусом R

А(-1; 0) ;  

(x -(-1))² + (y - 0)² = (√10)²

 (x + 1)² + y² = 10    -  уравнение окружности

2.б)  D(5; -2) :   (5 + 1)² + (-2)² = 36 + 4 = 40 ≠ 10

  Точка D не принадлежит окружности.

3. Каноническое уравнение прямой, проходящей через точку с координатами  (x₀; y₀) и направляющим вектором   :

 -  уравнение прямой

4.a) У коллинеарных векторов соответственные координаты пропорциональны.

Координаты пропорциональны, значит, векторы коллинеарны.

4.б) Так как векторы коллинеарны, значит, стороны  AB║CD.  Противоположные стороны параллельны и равны :

Скалярное произведение векторов   равно нулю, значит, векторы перпендикулярны, то есть ∠BAD=90°.

Итак, противоположные стороны параллельны и равны : AB║CD  и AB=CD, ∠BAD=90°  ⇒  ABCD - прямоугольник.