СРОЧНО!!!!!
f(x)=5sinx+cos2x [0;n]
Найти найбольшее и найменьшее значение функции на отрезке

Ответы

Ответ дал: WhatYouNeed

$f(x)=5sin{x}+cos{2x}\f'(x)=5cos{x}-2sin{2x}$

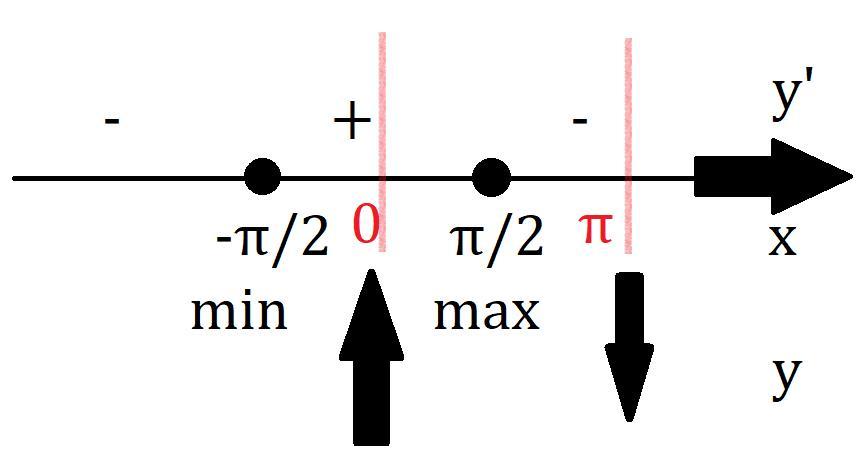
Найдём экстремумы и выделим нужный отрезок.

$f'(x)=4cos{x}(5/4-sin{x});|sin{x}|leq 1$

Значит экстремумы только в точках cos x =0

Значение в скобке всегда положительное.

См. вниз.

$f(x)_{max}=f(pi/2)=5-1=4\f(0)=5*0+1=1;f(pi)=5*0+1=1=>\f(x)_{min}=f(0)=f(pi)=1$

Ответ: Минимальное: 1.

Максимальное: 4.

Приложения:

Ответ дал: WhatYouNeed

Всё понятно?

Похожие вопросы

Окружающий мир

1 год назад

Русский язык

1 год назад

Другие предметы

2 года назад

Математика

2 года назад

Математика

8 лет назад

Математика

8 лет назад

Право

9 лет назад

Математика

9 лет назад