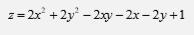Предмет: Алгебра
Автор: Tomoki
Вопрос задан 7 лет назад

< >

Найти экстремум функции двух переменных. Заранее спасибо.

Приложения:

Ответы

Ответ дал: Correlation

0

Найдем частные производные по переменным x, y:

$displaystyle frac{partial z}{partial x}=2cdot 2x-2y-2=4x-2y-2\ \ frac{partial z}{partial y}=2cdot 2y-2x-2=4y-2x-2$

Приравниваем частные производные к нулю:

$displaystyle left { {{4x-2y-2=0} atop {4y-2x-2=0}} right. ~~~Rightarrow~~~~+left { {{4x-2y-2=0} atop {8y-4x-4=0}} right. \ \ 8y-2y-2-4=0\ 6y=6\ y=1\ \ x=2y-1=2cdot 1-1=1$

Вычислим теперь частные производные второго порядка для построения матрицы Гессиана:

$displaystyle frac{partial^2z}{partial x^2}=4;~~~~~~~frac{partial^2z}{partial y^2}=4;~~~~~~frac{partial^2z}{partial xpartial y}=-2$

$displaystyle left(begin{array}{ccc}4&-2\ -2&4end{array}right)\ \ з_1=4>0\ \ з_2=left|begin{array}{ccc}4&-2\ -2&4end{array}right|=4cdot 4-(-2)cdot (-2)=16-4=12>0$

В точке (1;-1) имеется минимум $z(1;-1)=2cdot 1^2+2cdot (-1)^2-2cdot 1cdot(-1)-2cdot 1-2cdot (-1)+1=-1$

Похожие вопросы

Українська література

1 год назад

Українська література. Що означає чайка у вірші "чайка на крижині " автор Ліна Костенко. Допоможіть будьласка. Завчасно дякую.

Другие предметы

1 год назад

собливості світосприйняття головного героя пурпурові вітрила Дам 60 балов

Қазақ тiлi

2 года назад

кім? қайткен? нені? не? не істеді? кімге?

Қазақ тiлi

2 года назад

помогите пожалуйста очень срочно нужно сделать

Математика

8 лет назад

какую часть стены маляр красит за 1 час, если всю стену он покрасит за 3 3/5 часа?

Математика

8 лет назад

ширина участка земли прямоугольной формы 40 метров а длина 30м при выращивании одного сорта помидоров урожайность составила 9 кг/м2 сорт заменили другим урожайность которого была на одну третью

Химия

9 лет назад

химическая реакция получения водорода в промышленности

Геометрия

9 лет назад

з точки до даної площини проведено перпендекуляр і похилу . Похила на 1 см довша за перпендекуляр.Проекція похилої на площину 5см. Обислити довжину перпендикуляра