Окружность с центром О и радиусом 16 см описана около треугольника ABC так,что угол OAB =30 градусам,угол OCB=45 градусов .

найдите стороны AB и BC треугольника

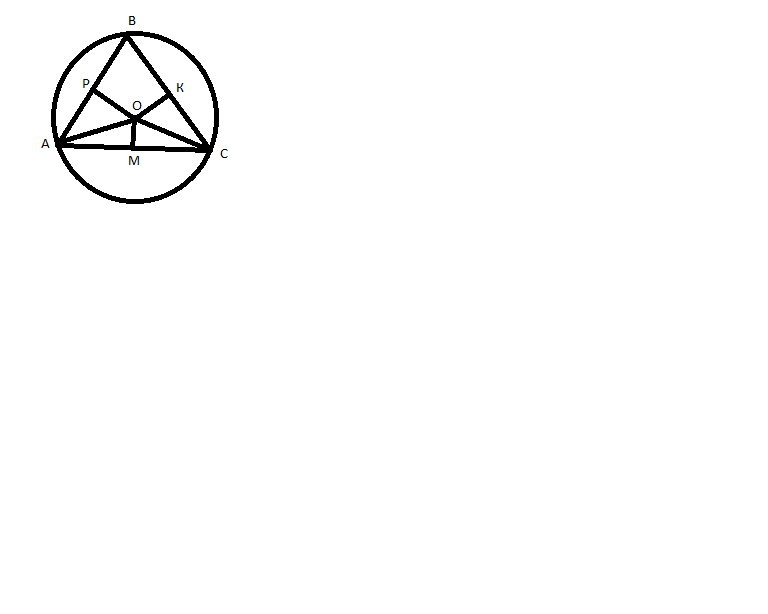
Около треугольника можно описать окружность, притом только одну. Её центром будет являться точка пересечения серединных перпендикуляров.
ОР, ОК, ОМ - серединные перпендикуляры, значит АР=РВ, ВК=КС, АМ=МС.
АО=r=16см
уголВАО=30градусов
в треугольникеАРО катет РО равен половине гипотенузы АО, т.к. лежит против угла 30 градусов. РО=16:2=8см
АР^2=16^2-8^2=256-64=192
АР=корень из192.
АВ=2*(корень из192)=2*(8корней из3)=16корней из3.

треугольник ОКС равнобедренный, т.к. уголОСК=45градусов, уголКОС=90-45=45градусов => ОК=КС (пусть =х)
х^2+х^2=16^2
2х^2=256
х^2=128
х=корень из128
КС=корень из128.
ВС=2*(корень из128)=2*(8корней из2)=16корней из2