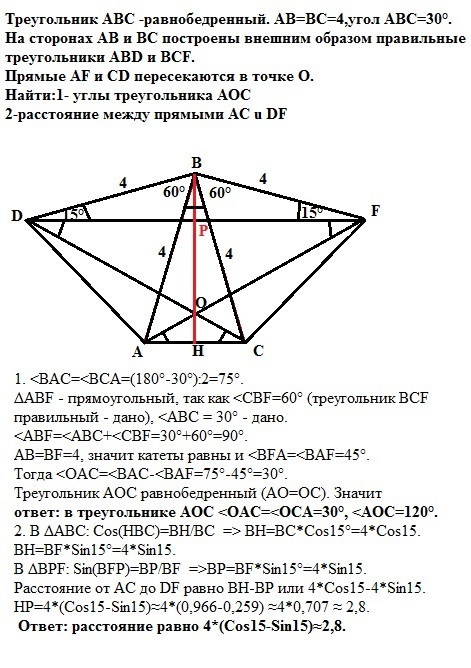
Треугольник ABC -равнобедренный. AB=BC=4,угол ABC=30 градусов.
На сторонах AB и BC построены внешним образом правильные треугольники ABD и BCF.
Прямые AF и CD пересекаются в точке О.
Найти:1- углы треугольника AOC
2-расстояние между прямыми AC u DF

1. <BAC=<BCA=(180°-30°):2=75°.
ΔABF - прямоугольный, так как <CBF=60° (треугольник BCF правильный
- дано), <ABC = 30° - дано.
<ABF=<ABC+<CBF=30°+60°=90°.
АВ=BF=4, значит катеты равны и <BFA=<BAF=45°.
Тогда <OAC=<BAC-<BAF=75°-45°=30°.
Треугольник АОС равнобедренный (АО=ОС). Значит
ответ: в треугольнике АОС <OAC=<OCA=30°, <AOC=120°.

2. В ΔABC: Cos(HBC)=BH/BC  => BH=BC*Cos15°=4*Cos15. BH=BF*Sin15°=4*Sin15.
В ΔBPF: Sin(BFP)=BP/BF  =>BP=BF*Sin15°=4*Sin15.
Расстояние от АС до DF равно ВН-ВР или 4*Cos15-4*Sin15.
НР=4*(Cos15-Sin15)≈4*(0,966-0,259) ≈4*0,707 ≈ 2,8.
Ответ: расстояние равно 4*(Cos15-Sin15)≈2,8.