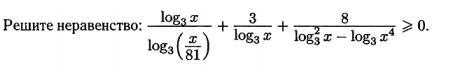Помогите решить неравенство

Ответ:

Пошаговое объяснение:

ОДЗ: x > 0, поэтому можно без напряга раскрывать модуль который образуется при 4log3 |x|

log3 (x/81) = log3 (x) - log3 (81) =  log3 (x) - 4

Пусть log3 (x) = t

t/(t - 4) + 3/t + 8/(t*(t - 4)) ≥ 0

После преобразования

(t^2 + 3t - 4)/(t(t - 4)) ≥ 0

Разложим квадратный трехчлен на множители

((t + 4)(t - 1))/(t(t - 4)) ≥ 0

t = -4

t = 1

t ≠ 0

t ≠ 4

 +            -             +            -             +

___-4_____0______1______4_____

log3 (x) ≤ -4

x ≤  1/81

с учетом ОДЗ

x ∈ (0; 1/81]

log3 (x) = 1

x = 3

log3 (x) = 0

x = 1

x ∈ (1; 3]

log3 (x) > 4

x > 81

x ∈ (81; + ∞)

Ответ: x ∈ (0; 1/81] U (1; 3] U (81; + ∞)