6. В треугольнике вторая сторона в два раза больше первой, а первая — на 2 м меньше третьей стороны,
причем периметр треугольника равен 42 м.
A) Найдите стороны треугольника.
Б) Найдите площадь квадрата, периметр которого равен периметру данного треугольника.
B) На стороне треугольника построен прямоугольник, периметр которого равен периметру
треугольника, а другая сторона прямоугольника, превосходит сторону обшую с треугольником.
Навате сторон ого пакетальника и периметр образовавшейся фигуры

А) Пусть х - длина первой стороны.
Тогда
2х - длина второй стороны;
х+2 - длина третьей стороны.
Р∆ = a+b+c - периметр треугольника, где a, b, c - длины его сторон.
По условию Р∆ = 42 м
Составляем уравнение:
42 = х + 2х + х + 2
4х = 42 - 2
4х = 40
х = 40 : 4
х = 10 м - длина первой стороны
2х = 2•10 = 20 м - длина второй стороны.
х + 2 = 10 + 2 = 12 м - длина третьей стороны.
Ответ: 10м; 20 м; 12 м.

Б) Ркв. = 4а - периметр квадрата, где а - длина стороны квадрата.
Дано:
Ркв. = Р∆
По условию Р∆ = 42 см.
4а = 42
а = 42 : 4 = 10,5 м - длина стороны квадрата, периметр которого равен периметру данного треугольника.
Sкв. = а•а - площадь квадрата, где а - длина стороны квадрата.
Sкв. = 10,5 • 10,5 = 110,25 кв.м - площадь квадрата, периметр которого равен площади данного треугольника.
Ответ: 110,25 кв.м.

В) Рпр. = 2(a+b) - периметр прямоугольника.
Дано:
Рпр. = Р∆
По условию Р∆ = 42 м.
2(a + b) = 42
a + b = 42 : 2
a + b = 21 м - полупериметр прямоугольника.
Предположим, что а - сторона, прямоугольника, общая со стороной прямоугольника, как это требуется в условии.
Тогда
b = 21 - a.
По условию b > a
то есть
21 - a > a
2a < 21
a < 21/2
a < 10,5 м - получается, что сторона, прямоугольника, общая со стороной прямоугольника не должна превышать 10,5 м
Из решения в пункте А известно, что длины сторон треугольника равны 10, 20 и 12 м.
Таким образом, мы выяснили, что прямоугольник построен на стороне треугольника, длина которого равна 10 м, и эта сторона меньшая.
Найдем
b = 21 - a
b = 21 - 10
b = 11 м - длина большей стороны прямоугольника.
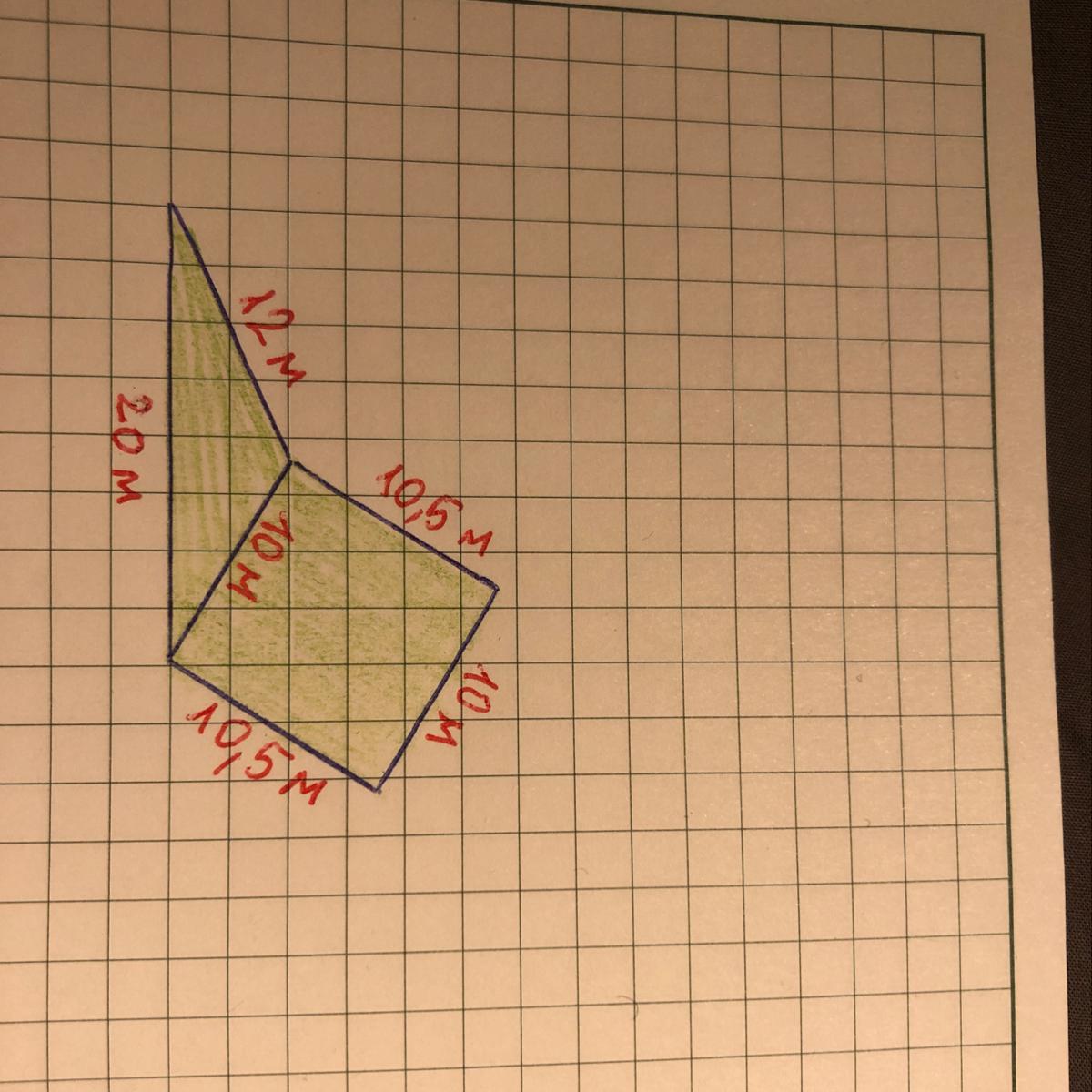
Таким образом, получилась фигура, называемая пятиугольником, и длины ее сторон равны соответственно:
20 м, 12 м, 10,5 м, 10м и 10,5 м.
Вычислим периметр этой фигуры:
Рфиг. = 20 + 12 + 10,5 + 10 + 10,5 = 63 м
Ответ: 63 м.