• Предмет: Алгебра
  • Автор: vladzorkov17
  • Вопрос задан 2 года назад
< >

Буду благодарен если поможете

Приложения:
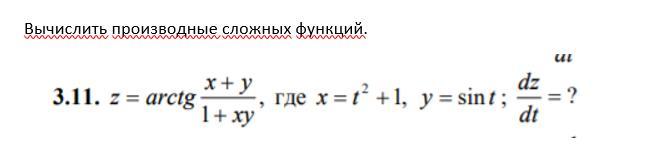
Simba2017: dz/dt=dz/dx*dx/dt-такое же возможно, с у -так же, а как их можно завязать между собой?
NNNLLL54: есть формулы производной сложной функции нескольких переменных

Ответы

Ответ дал: NNNLLL54
2

Ответ:

z=arctg\dfrac{x+y}{1+xy}\ \ ,\ \ \ x=t^2+1\ \ ,\ \ y=sint\\\\\\\boxed {\ z=z\Big(x(t)\ ;\ y(t)\Big)\ \ ,\ \ \ \ \dfrac{dz}{dt}=\dfrac{\partial z(x;y)}{\partial x}\cdot \dfrac{dx}{dt}+\dfrac{\partial z(x;y)}{\partial y}\cdot \dfrac{dy}{dt}\ }

\dfrac{dz}{dt}=\dfrac{1}{1+\dfrac{(x+y)^2}{(1+xy)^2}}\cdot \dfrac{1+xy-y(x+y)}{(1+xy)^2}\cdot 2t+\\\\\\+\dfrac{1}{1+\dfrac{(x+y)^2}{(1+xy)^2}}\cdot \dfrac{1+xy-x(x+y)}{(1+xy)^2}\cdot cost=\\\\\\=\dfrac{1-y^2}{(1+xy)^2+(x+y)^2}\cdot 2t+\dfrac{1-x^2}{(1+xy)^2+(x+y)^2}\cdot cost

Simba2017: спасибо Вам!
Simba2017: простите мою наглость, там еще один есть...
Simba2017: https://znanija.com/task/43758057
vladzorkov17: спасибо за помощь
Аноним: здравствуйте помогите пожалуйста с алгеброй
Похожие вопросы
Русский язык
1 год назад
напишите 6 предложений из художественной литературе повествовательное-2 предл. Вопросительное2предл. И пбудительное -2предл. Нужно срочно и их название с автором
Русский язык
1 год назад
эссе с деепречастиями обычаи и традиции казахов
Русский язык
2 года назад
ПРИМЕРЫ ПРЕДЛОЖЕНИЙ 6 КЛАСС СЕЙЧАС ОЧЕНЬ НУЖНО! СЛОЖНО СОЧИНЁННОЕ СЛОЖНО ПОДДЧИНЁННОЕ С ОБРАЩЕНИЕМ С ПРЯМОЙ РЕЧЬЮ БЕССЛЮЗНОЕ С ОДНОРОДНЫМИ ЧЛЕНАМИ МНОГО БАЛЛОВ!
Русский язык
2 года назад
Для чего мы употребляем в речи обращения ? В каких предложениях они чаще используются ? Почему ?
Математика
7 лет назад
Тесты помогите решить
Обществознание
7 лет назад
1. Подумай и объясни, какой смысл вложил А. С. Пушкин в своей фразе: "Сказка - ложь, да в ней намёк! Добрым молодцам урок”. 3. Как ты думаешь, почему первая детская энциклопедия в России вышла в
Химия
9 лет назад
Помогите решить цепочку
Математика
9 лет назад
решите последнее задание пожалуйста.....!!!!