решите интеграл❤️❤️❤️❤️​

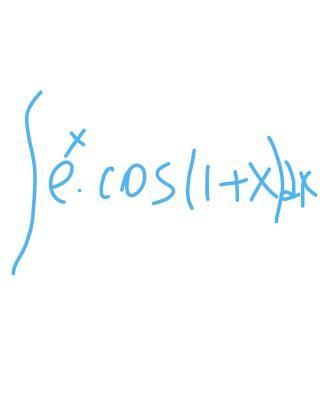
amanda2sempl: ∫eˣ cos(1+x)dx = ∫cos(1+x)deˣ = eˣcos(1+x) - ∫eˣdcos(1+x) = eˣcos(1+x) + ∫eˣsin(1+x)dx = eˣcos(1+x) + ∫sin(1+x)deˣ = eˣcos(1+x) + eˣsin(1+x) - ∫eˣdsin(1+x) = eˣcos(1+x) + eˣsin(1+x) - ∫eˣ cos(1+x)dx ⇒ ∫eˣ cos(1+x)dx = eˣcos(1+x) + eˣsin(1+x) - ∫eˣ cos(1+x)dx ⇒ 2∫eˣ cos(1+x)dx = eˣcos(1+x) + eˣsin(1+x) ⇒ ∫eˣ cos(1+x)dx = 0,5 * (eˣcos(1+x) + eˣsin(1+x))

amanda2sempl: Применяем прием: интегрирование по частям

amanda2sempl: ∫eˣ cos(1+x)dx = 0,5 * (eˣcos(1+x) + eˣsin(1+x)) + С, константу интегрирования нужно еще добавить