Ответы
Ответ дал:
2
Ответ:
решение смотри на фотографии
Приложения:
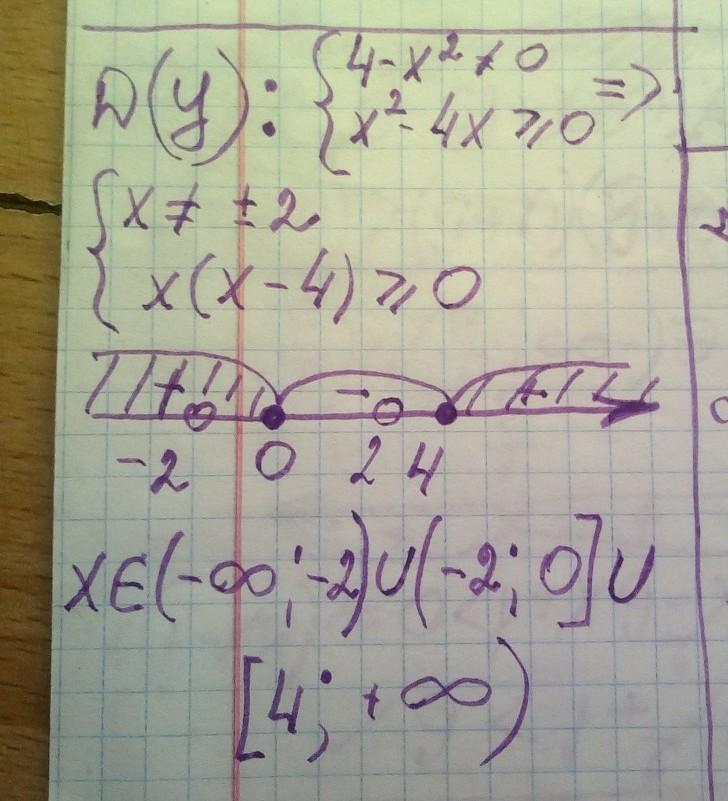
Ответ дал:
1
1) Знаменатель дроби не может быть равен нулю:
2) Выражение под корнем с четной степени не может быть отрицательным:
Приравняем к нулю и найдём, при каких значениях выражение равно нулю:
x = 0 или x - 4 = 0
x = 4
Значит при x = 0 и при x = 4 выражение x² - 4 равно нулю.
Коэффициент при x² положительный ⇒ ветви параболы направлены вверх. Значит нас удовлетворяют все значения x от минус бесконечности до нуля и от 4 до плюс бесконечности:
Учитывая то, что знаменатель дроби не может быть равен нулю, мы должны исключить из полученного ответа 2 и -2.
2 итак не входит, значит исключаем -2 и получаем окончательно:
Похожие вопросы
1 год назад
1 год назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
