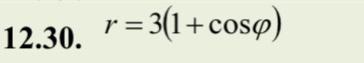Предмет: Алгебра
Автор: Xonda7777
Вопрос задан 1 год назад

< >

Вычислить площадь, ограниченную кривыми

Приложения:

Аноним: напишив телегу мені hahobn

Ответы

Ответ дал: NNNLLL54

2

Ответ:

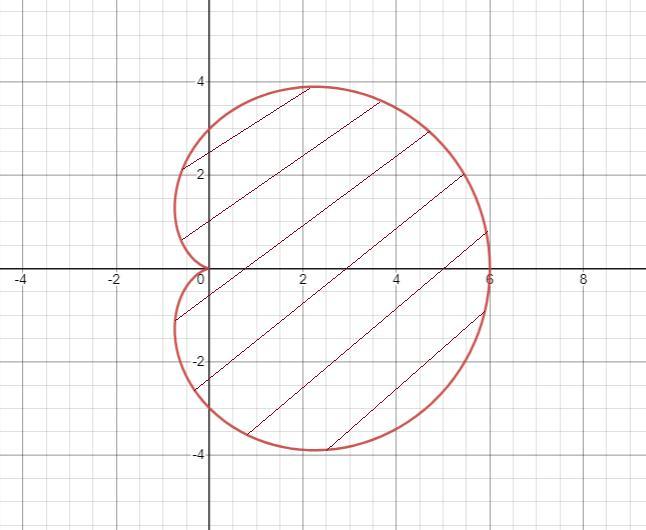
Площадь фигуры (кардиоиды) в полярных координатах .

$\displaystyle \bf r=3\, (1+cos\varphi )\\\\S=\frac{1}{2}\int\limits_0^{2\pi }\, r^2(\varphi)\, d\varphi =\frac{1}{2}\int\limits_0^{2\pi }\, 9\, (1+cos\varphi )^2\, d\varphi =\frac{9}{2}\cdot 2\int\limits_0^{\pi }\, (1+2cos\varphi +cos^2\varphi )\, d\varphi =\\\\\\=9\int\limits_0^{\pi }\, d\varphi +9\int\limits_0^{\pi }\, 2\, cos\varphi \, d\varphi +\frac{9}{2}\int\limits_0^{\pi }(1+cos2\varphi )\, d\varphi =$

$\bf \displaystyle =9\varphi \, \Big|_0^{\pi }+18\cdot sin\varphi \, \Big|_0^{\pi }+\frac{9}{2}\, \Big(\varphi +\frac{1}{2}\cdot sin2\varphi \Big)\Big|_0^{\pi }=\\\\\\=9\pi +18\cdot 0+4,5\pi +0=13,5\pi$

Приложения:

Xonda7777: Спасибо вам огромное

Похожие вопросы

Геометрия

1 год назад

помогите пожалуйста даю 50 60 балов

Химия

1 год назад

ПЖ СРОЧНО!! ДАЮ 55 БАЛЛОВ Укажите элемент,нуклонное число которого равна 52

Математика

1 год назад

Записать у вигляді періодичного десяткового дробу: А) 10*0,(7)=? Б) 10*6,(23)=? В) 0,(3)+0,(41)=?

Українська мова

1 год назад

1)Власне українські слова записано в рядку А.розум, добробут. Б.фактор,інтелект. В психолог, терапевт. Г.зоопарк,фото. 2)Лексичної помилки немає у реченні А.Уранці місто стоїть у пробках. Б.Наша

Русский язык

2 года назад

1.Прочитайте текст и письменно попытайтесь установить, какие местоимения в нём присутствуют. Давайте улыбнёмся! Улыбка-это нечто, чем встречают любого человека -не потому, что он хороший, умный,

Математика

2 года назад

Помогите с рещением лчень срочно

Литература

8 лет назад

Н.Н.Носов телефон кратко записать тему и главную мысль.

Математика

8 лет назад

Расстояние от кемпинга у моря до кемпинга у озера 155 км. Из обоих кемпингов навстречу друг другу выехали два велосипедиста и встретились через 5 часов. Скорость одного велосипедиста была 13 км/ч.