Угол AOB 40°, а угол BOC равен 70°. Чему равен угол между биссектрисами углов AOB и BOC? Если вариантов ответов несколько запишите в ответ их сумму

Решение .

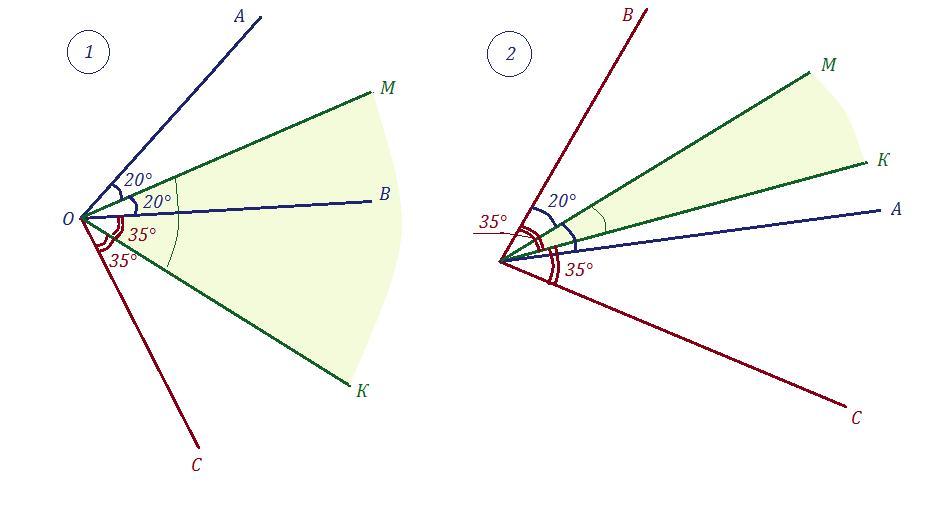
∠АОВ = 40°  ,  ∠ВОС = 70° ,  ОМ - биссектриса ∠АОВ ,        

ОК - биссектриса ∠ВОС  .

Найти угол между биссектрисами ОМ  и  ОК .

1)  Лучи ОА и ОС лежат по разные стороны от луча ОВ .

∠АОМ = ∠ВОМ = 20°  ,    ∠ВОК = ∠СОК = 35°  

Угол между биссектрисами  ∠МОК = ∠ВОМ + ∠ВОК = 20° + 35° = 55°    

2)   Луч ОА лежит внутри угла ВОС .

∠АОМ = ∠ВОМ = 20°  ,    ∠ВОК = ∠СОК = 35°  

Угол между биссектрисами  ∠МОК = ∠ВОК - ∠ВОМ = 35° - 20° = 15°  

Ответ:  сумма углов равна  55° + 15° = 70°  .