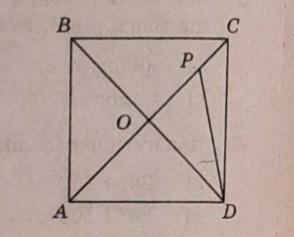
На рисунку АBCD- квадрат, точка Р належить відрізку СО, причому PD = 2PO. Знайдіть кут PDC. (НУЖНО ПОЛНОЕ РЕШЕНИЕ.)
Приложения:
Ответы
Ответ дал:
1
Ответ:
∠PDC=15°
Объяснение:
Діагоналі квадрата перетинаються перпендикулярно і точкою перетину поділяються навпіл, і є бісектрисами кутів.
∠СОD=90°; ∠ODC=45°
∆POD- прямокутний трикутник.
РD- гіпотенуза в два рази більше катета РО.
Катет РО лежить проти кута 30°
∠РDO=30°;
∠PDC=∠ODC-∠PDO=45°-30°=15°
zmeura1204:
Будь ласка.
:)
если чесно немного не понятно:(
Що саме?
Діагональ є бісектрисою. Кут ділемо навпіл ВDC=90/2=45°
∆POD; Катет проти кута 30°, тільки тоді він меньше гіпотенузи в два рази. ∠РDO=30°
45-30=15
почему в комментариях?
я не понимаю
Я все написала в розв'язку.
Похожие вопросы
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад