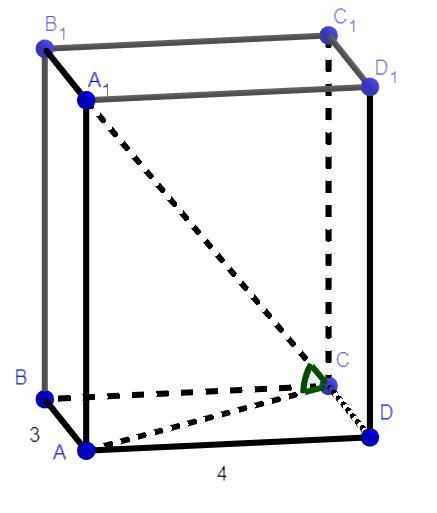
Стороны основания прямоугольного параллелепипеда равна 3 см и 4 см.Диагональ параллелепипеда наклонена к плоскости основания под углом 45 градусов.Найдите площадь полной поверхности параллелепипеда.

Сделаем чертеж. Диагональ основания определим по теореме Пифагора (тройки чисел). Она равна 5. Эта линия является проекцией диагонали параллелепипеда на плоскость основания, если рассмотреть тр-к этих линий, то мы увидим, что он прямоугольный и равнобедренный (угол 45),  высота параллелепипеда равна диагонали основания = 5.

S = 2(3+4)*5 + 2*3*4 = 94    (боковая поверхность - периметр умноженный на высоту + площадь двух оснований).

Ответ:

94 см²

Пошаговое объяснение:

Дано: ABCDA₁B₁C₁D₁ - прямоугольный параллепипед

AB = A₁B₁ = CD = C₁D₁ = 3 см

AD = A₁D₁ = BC = B₁C₁ = 4 см

∠A₁CA = 45° - угол между диагональю и плоскостью основания

Найти: Sполн

Решение:

Sполн = Sбок + 2·Sосн

Sбок = Pосн·h, h - высота параллелепипеда

Рассмотрим ΔADC - прямоугольный, ∠ADC = 90°, AD = 4, CD = 3

Найдём AC по теореме Пифагора

AC² = AD² + CD²

AC² = 4²+3² = 25

AC = 5 см

Рассмотрим ΔAA₁C

AA₁⊥ABCD ⇒ AA₁⊥AC ⇒ ΔAA₁C - прямоугольный

∠A₁AC = 90°, ∠A₁CA = 45° - по условию ⇒∠CA₁A = 45° ⇒ ΔAA₁C - равнобедренный, AA₁ = AC = 5

Pосн = 2(3+4) = 14 см

Sбок = 14 · 5 = 70 см²

Sосн = 3·4 = 12 см²

Sполн = 70+2·12 = 70+24 = 94 см²