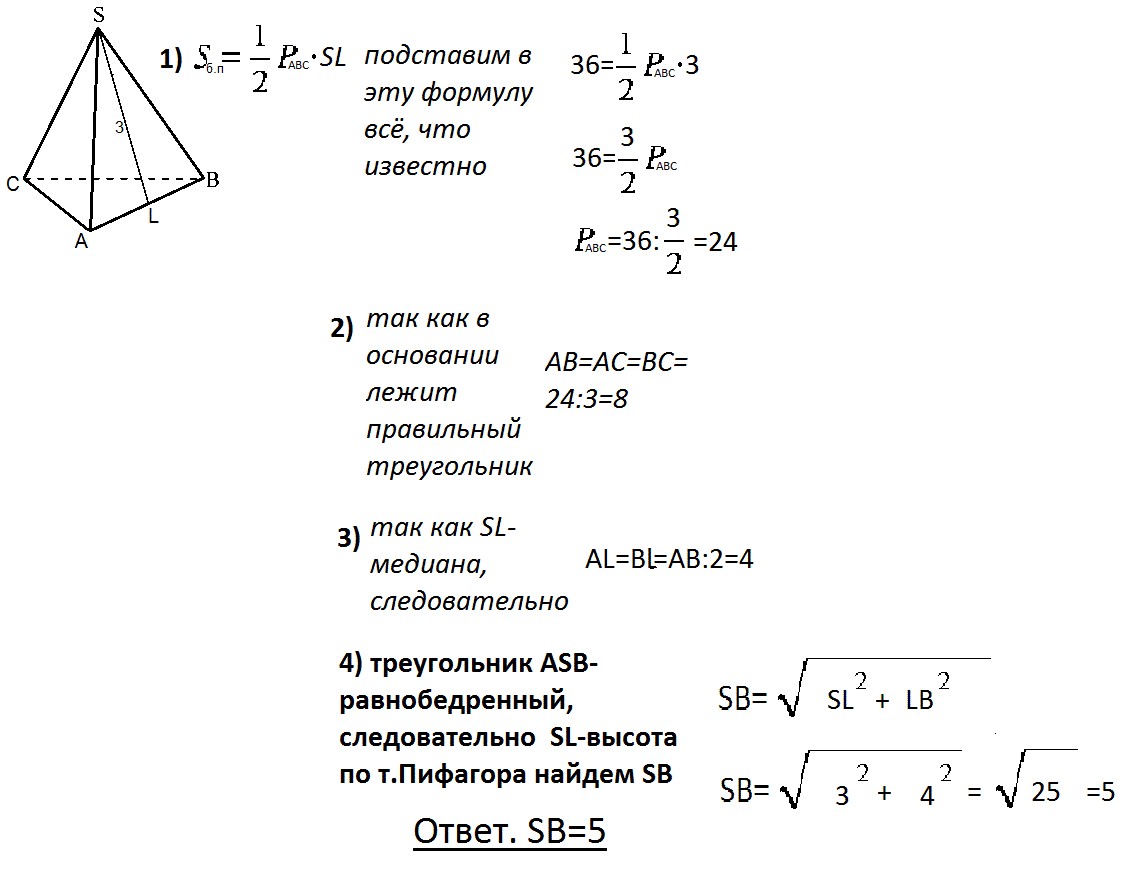
В правильной треугольной пирамиде SABC с вершиной S медиана SL треугольника SAB равна 3. Площадь всей боковой поверхности равна 36

Найдите длину отрезка SB. 

Sбок.=1/2*p*SL, где p=(AB+BC+AC):2;
подставив, получим
36=1/2*p*3 => p = 36*2:3=24;

т.к. в основании прав треугольник, то его сторона, допустим AB=p:3=24:3=8.

рассмотри треуг-к SAB, равнобедр, так как SA=SB, SL- медиана, проведенная к основанию, значит она и высота.
рассмотрим треуг-к SBL, прямоугольный, так как SL перпиндик BL. BL=1/2 AB=4 (так как по условию SL медиана).

и теперь по теореме Пифагора BS^2=BL^2+SL^2=16+9=25
BS=5. так как BS>0.

Решение с рисунком в вложении.