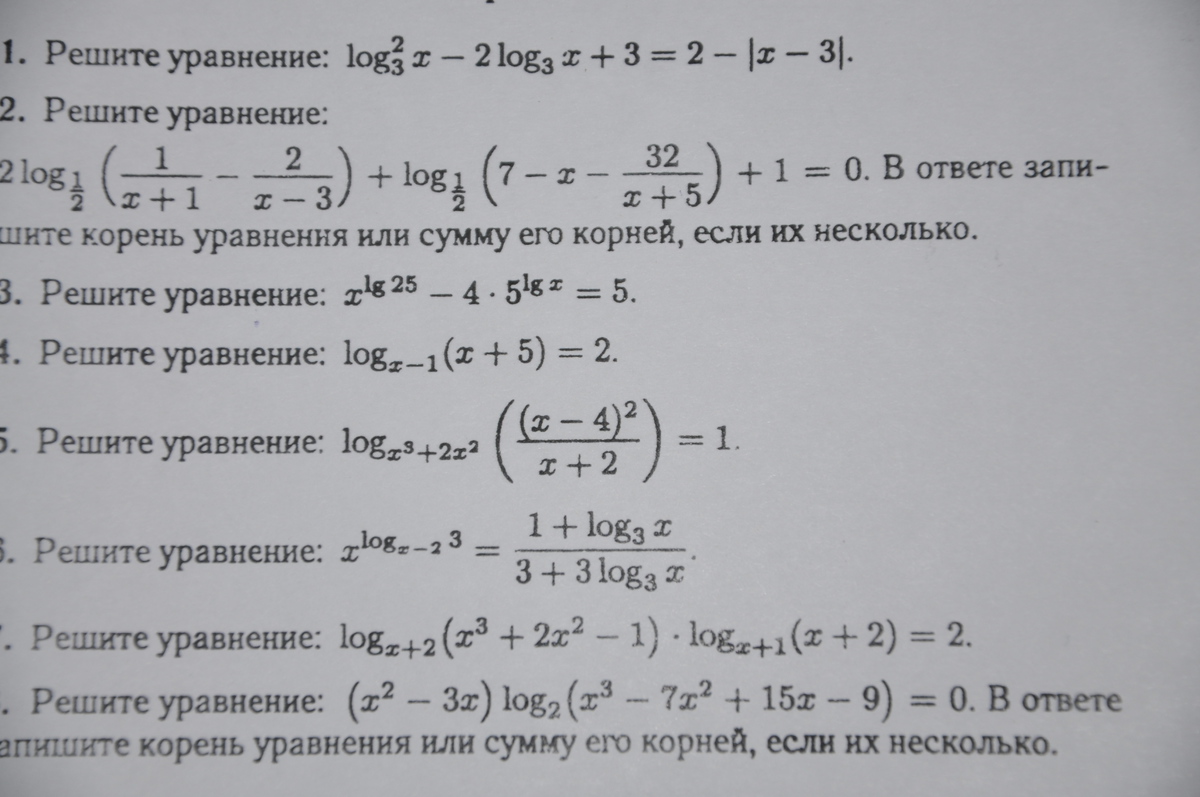Предмет: Алгебра
Автор: aloloy
Вопрос задан 9 лет назад

Логарифмические уравнения.

Приложения:

Ответы

Ответ дал: Artem112

$log_3^2x-2log_3x+3=2-|x-3| \ log_3^2x-2log_3x+1+2=2-|x-3| \ (log_3x-1)^2+|x-3|=0$
Сумма неотрицательных чисел равна 0 когда они оба равны нулю.
$log_3x=1; x=3 \ |x-3|=0; x=3$
Ответ: 3

$2log_{frac{1}{2}}(frac{1}{x+1}-frac{2}{x-3})+log_{frac{1}{2}}(7-x-frac{32}{x+5})+1=0 \ log_{frac{1}{2}}(frac{x-3-2(x+1)}{(x+1)(x-3)})^2+log_{frac{1}{2}}(frac{(7-x)(x+5)-32}{x+5})+1=0 \ log_{frac{1}{2}}frac{(-x-5)^2}{(x+1)^2(x-3)^2}+log_{frac{1}{2}}(frac{7x-x^2+35-5x-32}{x+5})+1=0 \ log_{frac{1}{2}}frac{(x+5)^2}{(x+1)^2(x-3)^2}+log_{frac{1}{2}}(frac{-x^2+2x+3}{x+5})+1=0 \ log_{frac{1}{2}}frac{(x+5)^2}{(x+1)^2(x-3)^2}+log_{frac{1}{2}}(-frac{(x-3)(x+1)}{x+5})+1=0$
$log_{frac{1}{2}}(-frac{(x+5)^2(x-3)(x+1)}{(x+1)^2(x-3)^2(x+5)})=-1 \ log_{frac{1}{2}}(-frac{x+5}{(x+1)(x-3)})=-1 \ -frac{x+5}{(x+1)(x-3)}=2 \ -x-5=2(x^2-3x+x-3) \ 2x^2-4x-6+x+5=0 \ 2x^2-3x-1=0$
Сами корни можно найти лишь с той целью, чтобы убедиться что при их подстановке в исходное уравнение оно не теряет смысла. Сумму же этих корней находим по теореме Виета, она равна -(-3)/2=1,5
Ответ: 1,5

$x^{lg25}-4cdot5^{lg x}=5 \ 25^{lg x}-4cdot5^{lg x}=5 \ (5^{lg x})^2-4cdot5^{lg x}-5=0 \ D_1=2^2+5=9 \ 5^{lg x} neq 2-3<0 \ 5^{lg x}=2+3=5 \ lg x=1 \ x=10^1=10$
Ответ: 10

$log_{x-1}(x+5)=2 \ (x-1)^2=x+5 \ x^2-2x+1-x-5=0 \ x^2-3x-4=0 \ (x-4)(x+1)=0 \ x_1=4; x_2=-1$
При подстановке второго корня в исходное уравнение получим отрицательное основание, чего не может быть - значит, это посторонний корень.
Ответ: 4

$log_{x^3+2x^2}( frac{(x-4)^2}{x+2} )=1 \ x^3+2x^2= frac{(x-4)^2}{x+2} \ x^2(x+2)^2=(x-4)^2 \ 1) x(x+2)=x-4 \ x^2+2x-x+4=0 \ x^2+x+4=0 \ D<0 \ 2) x(x+2)=4-x \ x^2+2x+x-4=0 \ x^2+3x-4=0 \ (x+4)(x-1)=0 \ x_1=-4; x_2=1$
При подстановке первого корня в исходное уравнение получаем отрицательное число в основании логарифма - посторонний корень.
Ответ: 1

$x^{log_{x-2}3}= frac{1+log_3x}{3+3log_3x} \ 3^{log_{x-2}x}= frac{1+log_3x}{3(1+log_3x)} = frac{1}{3} =3^{-1} (log_3x neq -1) \ log_{x-2}x=-1 \ (x-2)^{-1}=x \ frac{1}{x-2} =x \ x^2-2x=1 \ x^2-2x-1=0 \ D_1=1^2+1=2 \ x= 1pm sqrt{2}$
При подстановке корня $x_2=1- sqrt{2}$ основание логарифма отрицательно - это посторонний корень. При подстановке корня $x_1=1+ sqrt{2}>2.4$ уравнение обращается в верное равенство
Ответ: $1+ sqrt{2}$

$log_{x+2}(x^3+2x^2-1)cdot log_{x+1}(x+2)=2 \ frac{log{x+2}(x^3+2x^2-1}{log_{x+2}(x+1)} =2 \ log_{x+1}(x^3+2x^2-1)=2 \ (x+1)^2=x^3+2x^2-1 \ x^3+2x^2-1-x^2-2x-1=0 \ x^3+x^2-2x-2=0 \ x^2(x+1)-2(x+1)=0 \ (x+1)(x^2-2)=0 \ x=-1; x=pm sqrt{2}$
При подстановке найденных корней в уравнение получим, что только корень $x= sqrt{2}$ обращает его в верное равенство (при подстановке других корней получаем отрицательное основание или подлогарифмическое выражение)
Ответ: $sqrt{2}$

$(x^2-3x)log_2(x^3-7x^2+15x-9)=0$
Произведение равно нулю когда один из множителей равен нулю, а другой при этом не теряет смысла. Первый множитель равен нулю при х=0 и х=3, но эти значения обращают подлогарифмическое выражение в отрицательное или нулевое значения соответственно.
$log_2(x^3-7x^2+15x-9)=0 \ x^3-7x^2+15x-9=2^0=1 \ x^3-7x^2+15x-10=0 \ x^3-2x^2-5x^2+10x+5x-10=0 \ x^2(x-2)-5x(x-2)+5(x-2)=0 \ (x-2)(x^2-5x+5)=0$
Первый корень последнего уравнения равен 2, а сумма других других по теореме Виета равна 5. Следовательно, сумма всех корней уравнения равна 2+5=7
Ответ: 7

Похожие вопросы

Английский язык

2 года назад

Как сказать по Английски : откуда (из какой страны)они?откуда мы?откуда я?

Беларуская мова

2 года назад

ПОМОГИТЕ. ОЧЕНЬ НАДО!!!!!даю 50 пк надо написать сочинение по бел. яз. со словами(Ручаек, каменьчыки, з парожка на парожак, цянек, хмарка, зязюля, птушачки, гняздечки, коники(кузнечики), матыльки,

Информатика

7 лет назад

с какими типами ошибок вы встречались при создании программы в среде программированияscreatch

География

7 лет назад