Ответы
Ответ дал:
0
Ищем свободный делитель последнего чиста 12 ( 1 , -1 , 2 , -2 , 3 и т.д ) . За теоремой Безу делим в столбик на х-2 ( так как 2 подходит ) выйдет x^2-x-6 , дальше за т.Виета или дискриминантом , х1 = 3 , х2 = -2
Ответ дал:
0
х^3-3x^2-4x+12=0
Для решения уравнение разделим его на один из его корней, корень ищем среди делителей свободного члена. В данном случае это 12
12 Делители:
+1 -1 +2 -2 -3 +3 +4 - 4 +6 - 6 +12 - 12
2 подходит
Делим
х^3-3x^2-4x+1 на x-2 (смотри рисунок)
получаеться(x-2)(x^2-x-6)=0
Решаем: x^2-x-6
D=b^2-4*a*c = 1+24 = 25
x1=-2
x2=3
(x-2)(x-3)(x+2)=0
Произведение корней : -2*2*3 = -12
Ответ: -12
Приложения:
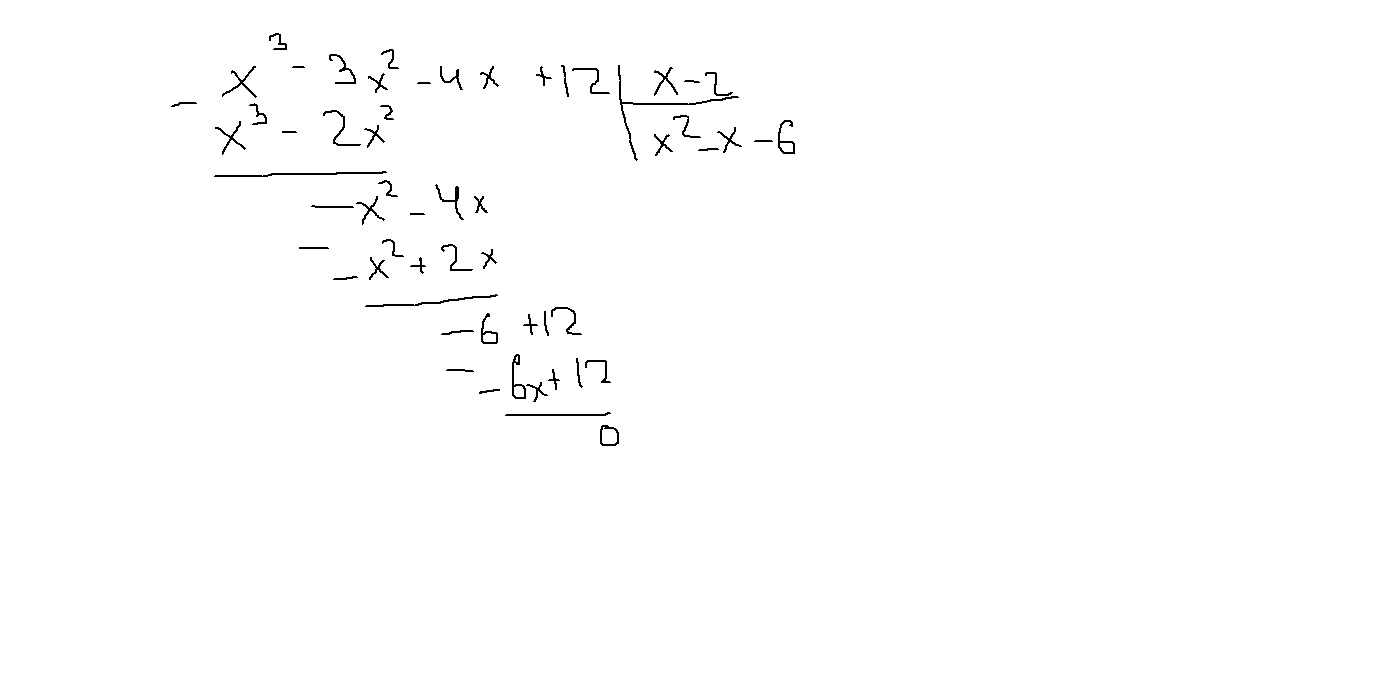
Похожие вопросы
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад