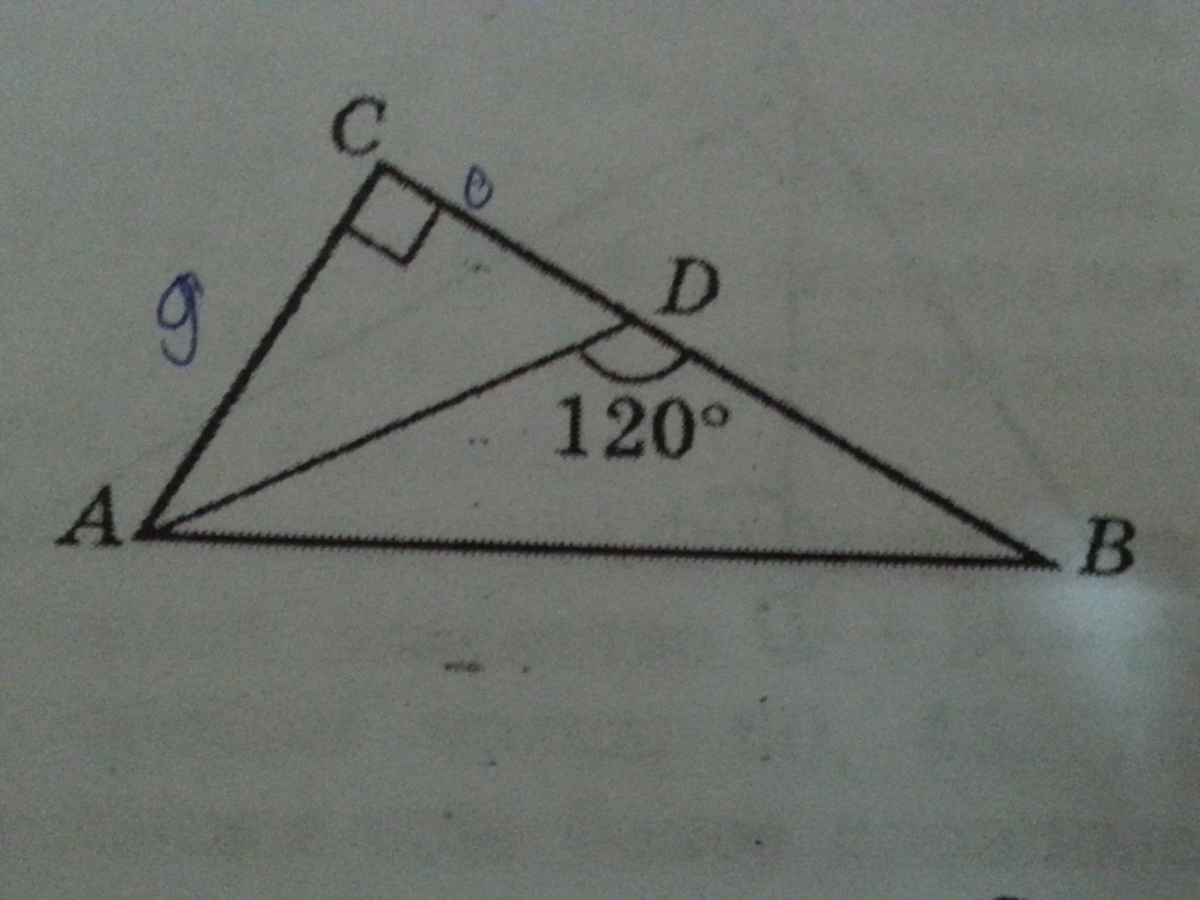
СРОЧНО! Помогите решить задачу по теореме Пифагора: Треугольник АBС - прямоугольный.Угол АDB=120 градусов, СD=6, АД=БД.Найти AB.
Приложения:
Ответы
Ответ дал:
0
1) Угол ADC = 60 = 180 - 120(cмежные)
2) Угол DAC = 30 = 180 - 60 - 90(сумма углов треугольника равна 180)
3)Сторона AD = 2CD(теорема: сторона лежащая на против угла в 30 градусов, равна половине гипотенузы => гипотенуза равна 2ум таким сторонам )
AD = 12
AD = BD (из условия)
Проведем высоту из вершины D на сторону AB = DH (она является и биссектрисой и медианой и высотой)
Угол ADH = 60(120/2 так как биссектриса) => Угол DAH = 180 - 90 - 60 = 30
И снова угол в 30 градусов => DH=(1/2)AD = 6
Найдем AH(по теореме пифагора) = (144-36)^(1/2(корень)) =
AB = 2AH =
2) Угол DAC = 30 = 180 - 60 - 90(сумма углов треугольника равна 180)
3)Сторона AD = 2CD(теорема: сторона лежащая на против угла в 30 градусов, равна половине гипотенузы => гипотенуза равна 2ум таким сторонам )
AD = 12
AD = BD (из условия)
Проведем высоту из вершины D на сторону AB = DH (она является и биссектрисой и медианой и высотой)
Угол ADH = 60(120/2 так как биссектриса) => Угол DAH = 180 - 90 - 60 = 30
И снова угол в 30 градусов => DH=(1/2)AD = 6
Найдем AH(по теореме пифагора) = (144-36)^(1/2(корень)) =
AB = 2AH =
Ответ дал:
0
<ADC=180-<ADB=180-120=60-смежные⇒<CAD=90-<ADC=90-60=30-сумма острых углов прямоугольного треугольника⇒CD=1/2AD=6⇒AD=2CD=12
AD=DB по условию⇒CB=CD+DB=6+12=18
AC=√(AD²-CD²)=√(144-36)=√108=6√3
AB=√(AC²+CB²)=√(108+324)=√432=72√3
AD=DB по условию⇒CB=CD+DB=6+12=18
AC=√(AD²-CD²)=√(144-36)=√108=6√3
AB=√(AC²+CB²)=√(108+324)=√432=72√3
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад